Theory of Geometric Unity

The Theory of Geometric Unity is an attempt by Eric Weinstein to produce a unified field theory by recovering the different, seemingly incompatible geometries of fundamental physics from a general structure with minimal assumptions.

• A first video presentation of the theory is available on Youtube
• A transcript of the talk is available here.
• Preliminary notes by the community on the talk are available in a Google Doc
• Discussion on the Joe Rogan show
• PBS SpaceTime

"The source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language." - Eric Weinstein

Project Ideas

• Unpack Eric's first talk by providing additional explanations for the concepts and problems introduced. One possible format would be to annotate it in a Genius.com format.
• Organize voice/video chats to watch the talk together and stop every few minutes to discuss it. (Multiple calls would be needed to go through the whole talk.)

Key Ideas

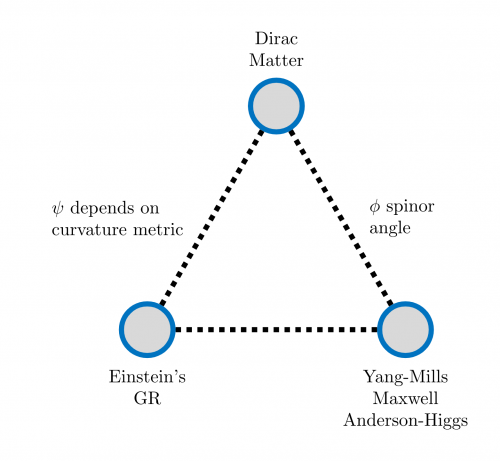
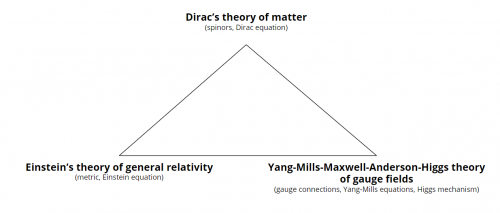
Starting point: three observations by Edward Witten

1. The Arena (<math> X, g_{\mu\nu}</math>)	<math>R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \left( \dfrac{8 \pi G}{c^4} T_{\mu\nu}\right)</math>	the Einstein field equations, which describe gravity in the theory of general relativity
2. <math>G</math> (non abelian) <math> SU(3) \times SU(2) \times U(1)</math>	<math>d_A^*F_A=J(\psi)</math>	the Yang-Mills equation, which governs all other force fields in Yang-Mill-Maxwell theory
3. Matter Antisymmetric, therefore light	<math>(i \hbar \gamma^\mu \partial_\mu - m) \psi = 0</math>	the Dirac equation, the equation of motion describing matter particles, or fermions

Key guiding question: what are the compatibilities and incompatibilities between these puzzle pieces on the geometric level before the theory is created quantum mechanical.

Problem Nr. 1: Einstein's Theory of General Relativity is not a proper Gauge Theory

• From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection $$\nabla$$ of the metric $$P_E(F_{\nabla})$$
• From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection $$d^\star_A F_A$$

Idea: What if the $$F$$'s are the same in both contexts?

Further, supposing these $$F$$'s are the same, then why apply two different operators?

Thus the question becomes: Is there any opportunity to combine these two operators?

A problem is that the hallmark of the Yang-Mills theory is the freedom to choose the data, the internal quantum numbers that give all the particles their personalities beyond the mass and the spin. We can allow the gauge group of symmetries to act on both sides of the equation, but the key problem is that: $$P_E(F_{\nabla h}) \neq h^{-1} P_E(F_{\nabla}) h $$. If we act on connections on the right and then take the Einstein projection, this is not equal to first taking the projection and then conjugating with the gauge action. The gauge rotation is only acting on one of the two factors. Yet the projection is making use of both of them. So there is a fundamental incompatibility in the claim that Einstein's theory is a gauge theory relies more on analogy than an exact mapping between the two theories.

Problem Nr. 2: Spinors are sensitive to the metric

Observation: Gauge fields do not depend on the existence of a metric. One-forms are defined whether or not a metric is present. But for spinors (fermion fields) this is not the case.

"So if we're going to take the spin-2 $$G_{\mu\nu}$$ field to be quantum mechanical, if it blinks out and does whatever the quantum does between observations. In the case of the photon, it is saying that the waves may blink out, but the ocean need not blink out. In the case of the Dirac theory, it is the ocean, the medium, in which the waves live that becomes uncertain itself. So even if you're comfortable with the quantum, to me, this becomes a bridge too far. So the question is: "How do we liberate the definition?" How do we get the metric out from its responsibilities? It's been assigned far too many responsibilities. It is responsible for a volume form; for differential operators; it's responsible for measurement; it's responsible for being a dynamical field, part of the field content of the system."

Comments

Mark-Moon: Can anyone explicate Eric's point about spinor fields depending (in a bad way) on the metric in conventional theories, in a way that is no longer the case in GU? I feel like this is the original idea in GU that I'm closest to being able to understand, but I don't think I quite get it yet.

Chain: Yeah I was wondering this as well, as far as I was aware you just need a spin structure, which only depends on the topology and atlas on the manifold and not on the choice of metric [1]. Perhaps the point is that although each choice of metric yields an isomorphic spin structure, perhaps there is not a canonical isomorphism in the same way as in GU where the bundle of metrics Y (U in the talk) is isomorphic to the Chimeric bundle C, but the choice of isomorphism is given by a choice of connection on Y. Although I don't know why the chimeric bundle would come with a canonical choice of spin structure either, which seems to be Eric's claim to define spinors you would need a clifford bundle and hence a choice of metric on the chimeric bundle

Problem Nr. 3: The Higgs field introduces a lot of arbitrariness

"The Dirac field, Einstein's field, and the connection fields are all geometrically well-motivated but we push a lot of the artificiality that we do not understand into the potential for the scalar field that gives everything its mass. We tend to treat it as something of a mysterious fudge factor. So the question is, if we have a Higgs field: "why is it here and why is it geometric?""

Proposed Solution

We may have to generalize all three vertices before we can make progress. That's daunting because in each case, it would appear that we can make an argument that the three vertices are already the simplest possible theories that could live at these vertices.

• We know, for example, the Dirac operator is the most fundamental of all the elliptic operators and Euclidean signature generating all of the Atiyah-Singer theory.
• We know that Einstein's theory describes, in some sense, a unique spin two massless field capable of communicating gravity, which can be arrived at from field-theoretic rather than geometric consideration.
• In the Yang-Mills case, it can also be argued that the Yang-Mills theory is the simplest theory that we can write down. In the Yang-Mills case, we have no substructure, and so we're doing the most simple-minded thing we can do by taking the norm-squared of the curvature and saying whatever the field strength is, let's measure that size.

So if each one of these is simplest possible, doesn't Occam’s razor tell us that if we wish to remain in geometric field theory, that we've already reached bottom?

I would say that there are other possibilities that while each of these may be simplest in its category, they are not simplest in their interaction.

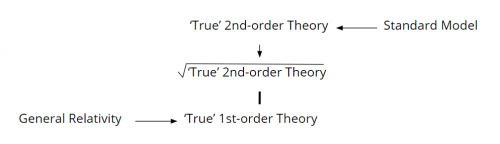
For example, we know that Dirac famously took the square root of the Klein-Gordon equation to achieve the Dirac equation. He actually took two square roots, one of the differential operator, and another of the algebra on which it acts. But could we not do the same thing by re-interpreting what we saw in Donaldson theory and Chern-Simons theory and finding that there are first-order equations that imply second-order equations that are nonlinear in the curvature?

So, let's imagine the following: we replaced the standard model with a true second-order theory. We imagine the general relativity is replaced by a true first-order theory. And then we find that the true second-order theory admits of a square root and can be linked with the true first order theory.

This would be a program for some kind of unification of Dirac's type, but in the force sector. The question is, "does this really make any sense? Are there any possibilities to do any such thing?"

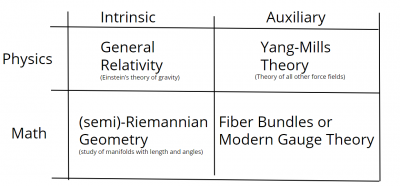
Let's talk about what the Geometric Unity (GU) proposal is. First of all, we observe that we have a division into intrinsic theories and auxiliary theory and between physics and mathematics. And intrinsic physical theory would be general relativity. An auxiliary physical theory would be the Yang-Mills theory, with the freedom to choose internal quantum numbers.

At the mathematical level, an intrinsic theory would be, the older semi-Riemannian geometry. The study of manifolds with length and angle. Auxiliary geometry is what we're going to call fiber bundle theory or modern gauge theory.

Geometric Unity is the search for some way to break down the walls between these four boxes.

What we'd like to come up with is some theory that is intrinsic, but allows us to play some of the games that exist in other boxes. How can we fit? How can we try to have our cake and eat it too? And use all the full suite of techniques that are available to us?

Our perspective is that the quantum that may be the comparatively easy part and that the unification of the geometry, which has not occurred, may be what we're being asked to do.

Frequently Asked Questions

What will this theory predict?

When will Eric release the next part?

On the Lex Fridman Podcast, Eric states that he may release a paper on April Fool's day, 2021 on the topic of Geometric Unity.

Why hasn't Eric gone through the normal scientific route? Arxiv.org? Academic journals?

Answer: He is planning on releasing his theory through the traditional route of publishing an academic paper in the near future. He is unlikely to publish in any academic journal that has a paywall - he has voiced concerns over price gouging that many academic journals engage in.

Related existing theories

Causal Fermion Systems: [2]