User:Aardvark/GWT

From The Portal Wiki
< User:Aardvark
Revision as of 21:55, 27 October 2020 by Aardvark (talk | contribs)
Jump to navigation Jump to search

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Pellentesque commodo efficitur facilisis. Donec ut blandit massa, scelerisque aliquet leo. Nullam nec erat ipsum. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Nam faucibus nulla ac libero lobortis volutpat. Vestibulum mauris mi, auctor sit amet ultrices vel, laoreet id quam. Vivamus ut augue est. Ut eu quam dui. Curabitur scelerisque lectus eu dolor luctus, a malesuada libero suscipit. Quisque lobortis ornare neque in ultricies. Praesent et eros id odio ullamcorper sodales. Proin quis ornare metus. Nam hendrerit tortor ac dapibus eleifend.

Pellentesque scelerisque justo nec aliquam commodo. Suspendisse luctus varius aliquam. Proin lacus nisi, fringilla sit amet pulvinar ut, mollis vitae massa. Duis eleifend semper mi sit amet tempus. Aliquam eget nisl sodales, congue ligula ut, lacinia justo. Quisque cursus velit eu commodo condimentum. Mauris nec sagittis tortor. Donec at fringilla elit. Proin vulputate quis orci sed aliquam. Ut dignissim elit luctus ligula faucibus lacinia. Donec eget augue diam. Interdum et malesuada fames ac ante ipsum primis in faucibus. Donec congue odio ut condimentum fermentum.

Prime Directive

A request:

Try to draw the lines through the three. View it as a unified idea:

The Paragraph gets edited,

The Wall gets defaced and graffitied,

The Sacred Tome gets rewritten.

But follow the skeins through each.

The Graph points to the Wall,

And the Wall to the Tome,

And the Tome leads to the Search.

Graph

The Graph is a paragraph from Edward Witten's paper Physics and Geometry, at the bottom of page 20:

If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations:

(i) Spacetime is a pseudo-Riemannian manifold $$M$$, endowed with a metric tensor and governed by geometrical laws.

(ii) Over $$M$$ is a vector bundle $$X$$ with a non-abelian gauge group $$G$$.

(iii) Fermions are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}_{-} \otimes V_{\tilde{R}})$$. $$R$$ and $$\tilde{R}$$ are not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in representation difference $$\Delta$$ in some underlying theory.

All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.

The-graph.png

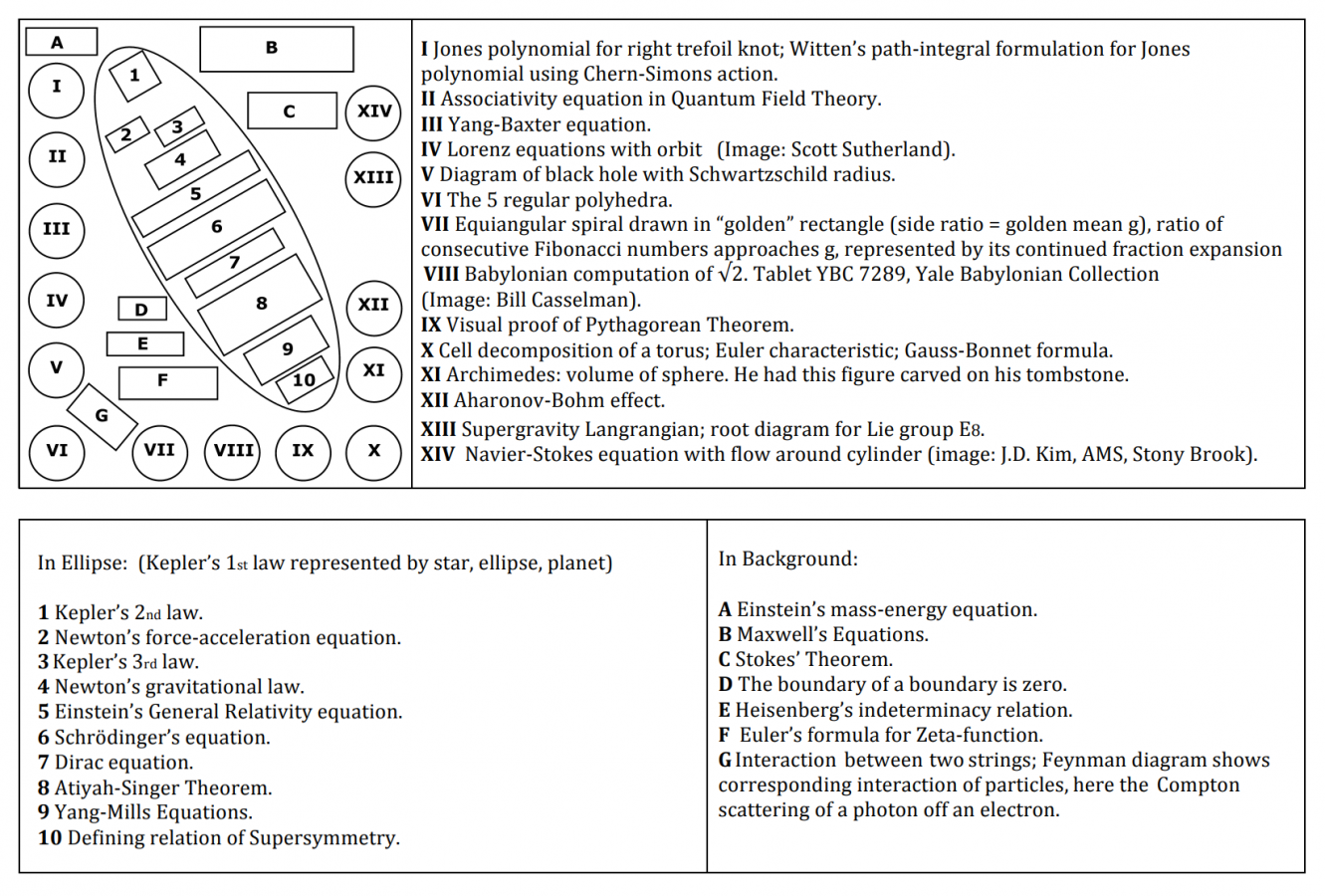
Wall

The following image is carved into a wall at Stony Brook University. It contains many equations and mathematical results that have contributed to the human understanding of reality.

click here for an interactive version of the Wall.

  • The Wall

  • Explanations for the Wall

Tome

The Road to Reality
The-tome.png
Information
Author Sir Roger Penrose
Language English
Genre Physics
Publisher Vintage
Publication Date 9 January 2007
Pages 1136

The Tome is The Road to Reality by Sir Roger Penrose, which contains a comprehensive account of the physical universe. To gain an understanding and intuition for the information contained in 'The Graph', and 'The Wall', reading this book will provide a great head-start. With 34 chapters spread over 1000 pages, including diagrams, equations, and descriptions, there are multiple avenues for understanding all concepts.

Study notes for the Tome can be found here.

Reference material by chapter can be found here.

Core Sub-projects

Editing the Graph

Editing the Graph - The goal is to create an updated version of the Graph since there are several small aspects of it that can and should be improved.

Defacing the Wall

Rewriting the Tome

Resources

Other Sub-projects

  • Studying the Tome - The Tome can be intimidating. This problem can be solved 1.) by creating resources that make it easier to digest its content and 2.) by going through the chapters together.
  • Geometry Project - The aim is to create and collect resources related to Frederic P. Schuller's lecture series titled "Lectures on Geometrical Anatomy of Theoretical Physics" that provides a great introduction to geometrical concepts that are essential for the Graph, Wall, Tome project.
  • Holonomy Project - The goal is to create visualizations for the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.

Reference

OLD Further Project Ideas

  • Organize expeditions - (guided or unguided) tours through the portal and into the wonderful world we call physics. Intellectual tourism.
  • Create/assemble resources that provide a geometric intuition for the equations and principles of fundamental physics - Geometric interpretations are most amenable to being visually represented. An example, is shown here.
  • Create Accelerators: 2 minute guides to fundamental principles.
  • Create/assemble resources that allow uninitiated to quickly and easily get up to speed with state of the project.
  • Create/assemble resources that provide analogies for more complex principles - to demonstrate a key feature of the principle.
  • Annotate/colorize the most important equations
  • Publish discussions and comments on chapters of the Tome.
  • Publish study guide for the Tome.
  • Publish roadmaps for navigating through the Tome.
  • Create dependency graphs for chapters of the Tome.
  • Create expandable version of the Graph, i.e. multiple versions of the Graph that reveal more and more details.
  • Create fully-fledged learning path like [1]

OLD Resources & References

Retrieved from ‘https://old.theportal.wiki/wiki?title=User:Aardvark/GWT&oldid=7263’