Decoding the Graph-Wall-Tome Connection

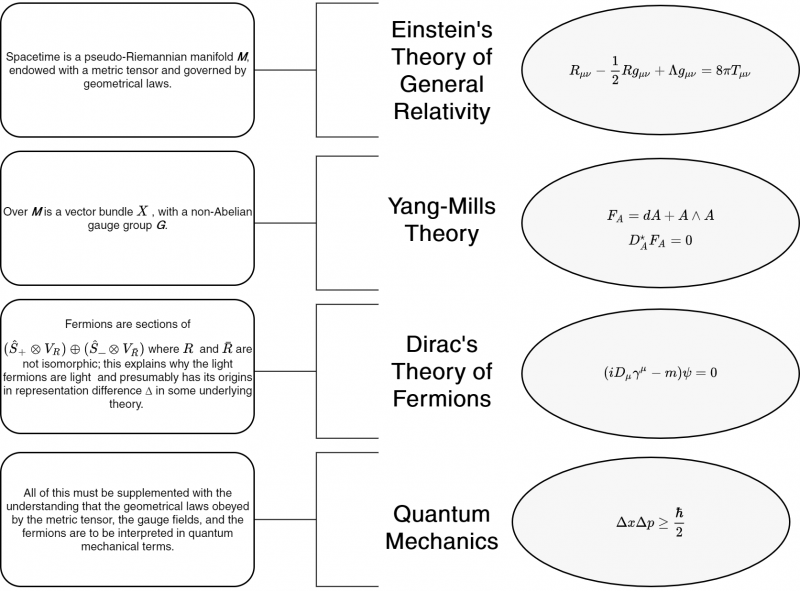
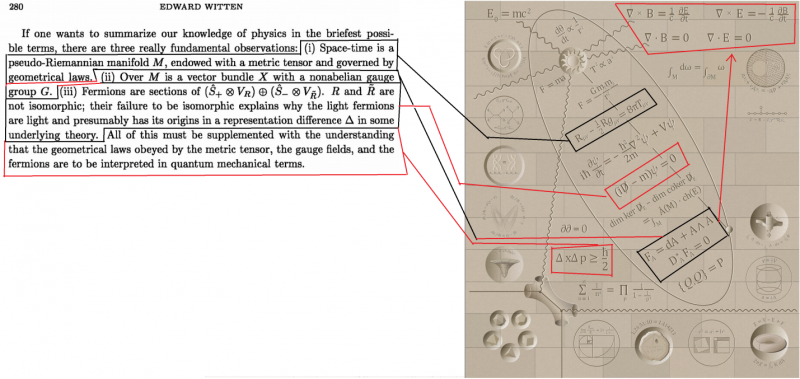
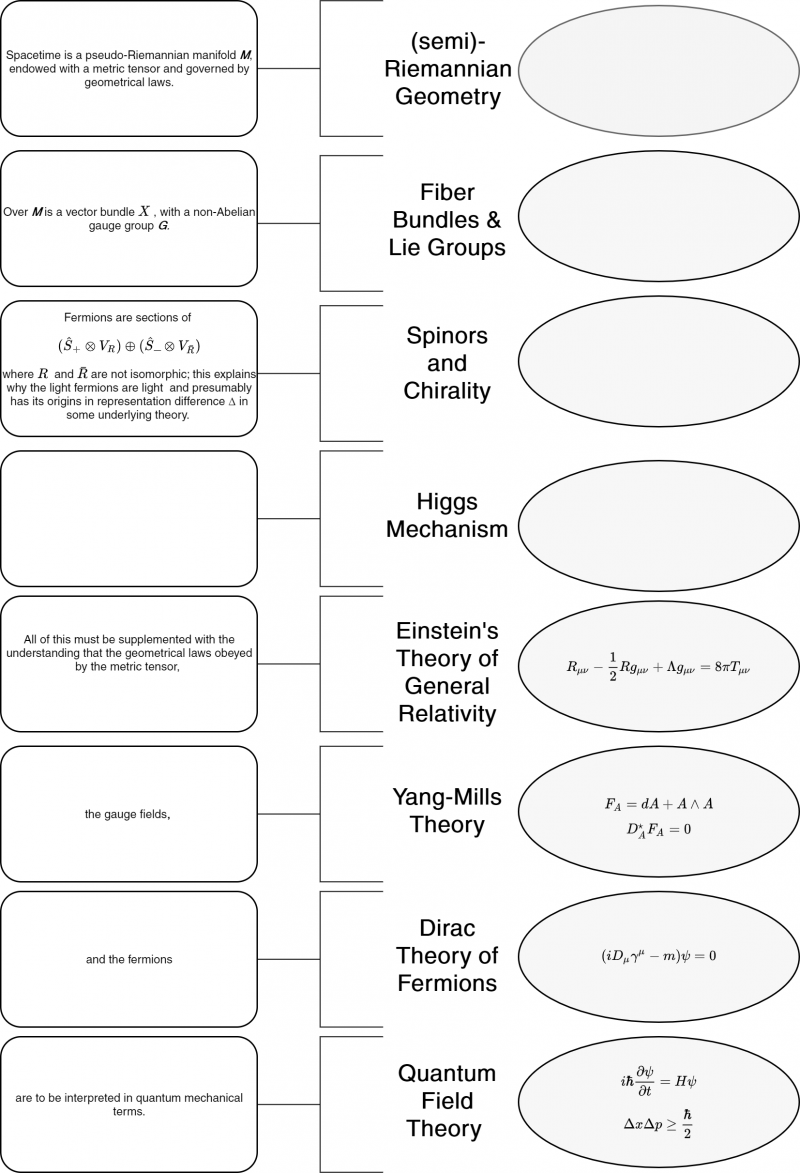
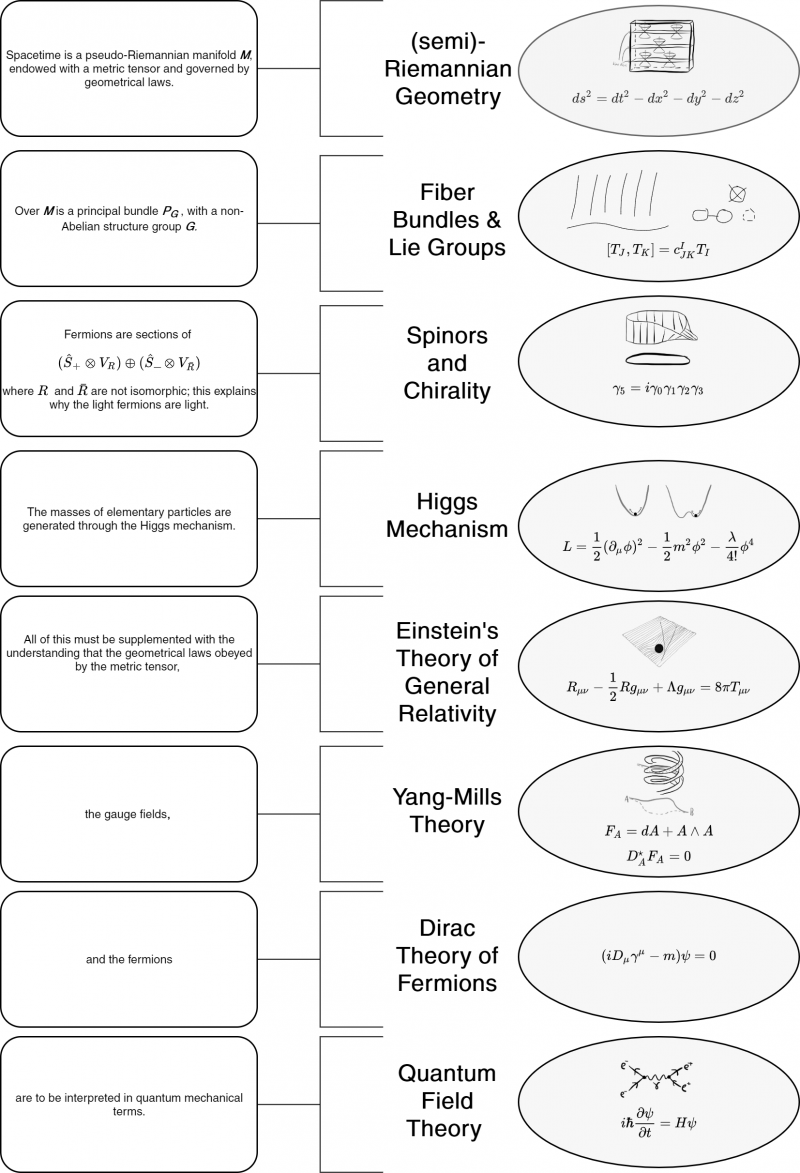
An important aspect of the prompt is that neither the Graph, nor the Wall or the Tome are that important.

What really matters are the common threads that run through all of them.

The goals of this project are to:

• Identify the common threads (the "unifying idea") in the Graph, Wall, and Tome.
• Create and collect resources that make it easy to understand them.

Database Information

Guiding Questions and Comments by Eric Weinstein

What is $$F_A$$ geometrically?

$$F_A$$ is the curvature tensor associated to the connection or vector potential $$A$$.

What are $$R_{\mu v}$$ and $$R$$ geometrically?

Explanation of $$R$$

$$R$$ is a scalar value, describing the "curvature of the spacetime manifold" at each point along the manifold. It's based on a concept of 'parallel transport', where you move a vector around some path on the manifold.

$$R$$ can be computed at each point on the manifold, and describes the difference in the vector's angle after following an infinitesimally small path around the neighborhood of that point, vs. what it was originally. The video does a great job of visualizing when and why that vector angle change would happen, with flat vs. curved manifolds.

In the video, they focus first on the curvature of space. Hopefully they incorporate back in curvature in time, because that's less obvious.

The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts.

Further thoughts on the meaning of R

How do they relate?

Cohomology

What does this have to do with Penrose Stairs?

• Penrose stairs
• Spinor

We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.

What are “Horizontal Subspaces” and what do they have to do with Vector Potentials or Gauge fields?

• Vertical and horizontal bundles
• Introduction to gauge theory
• Symmetry

From theplebistocrat:

Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.

Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.

But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.

"The source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language." - Eric Weinstein

• Another valuable resource is the comments Eric made regarding how the Wall should be modified.

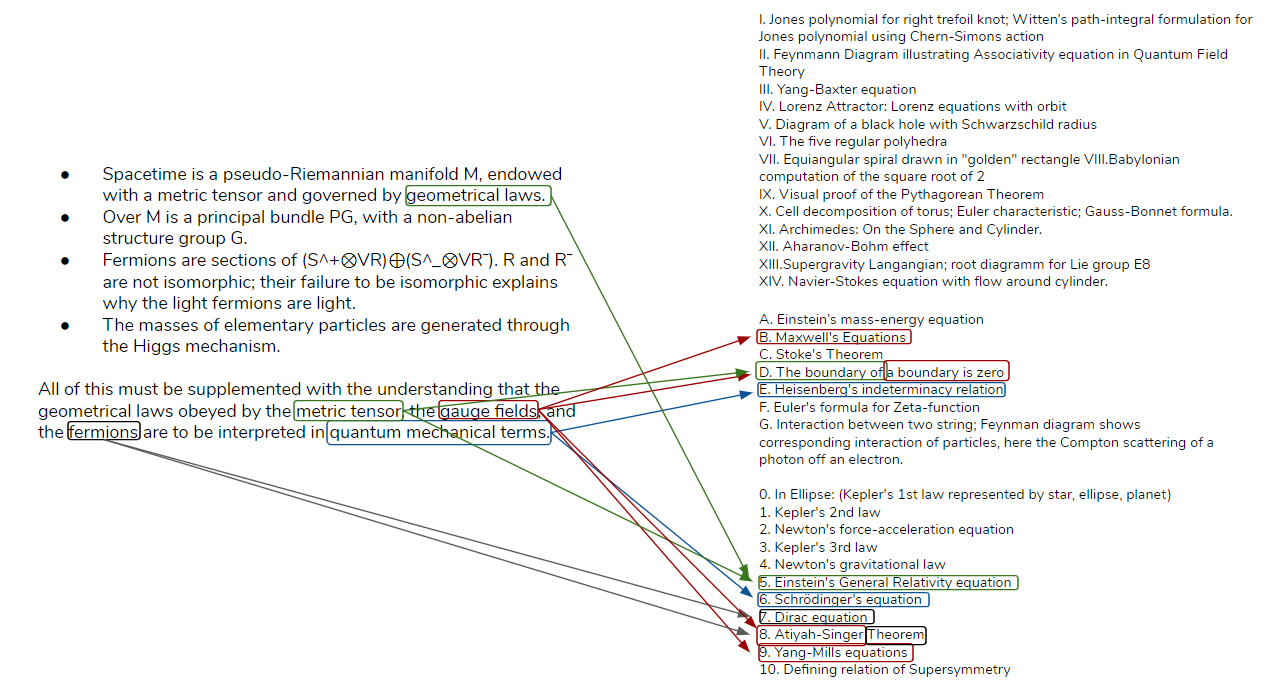
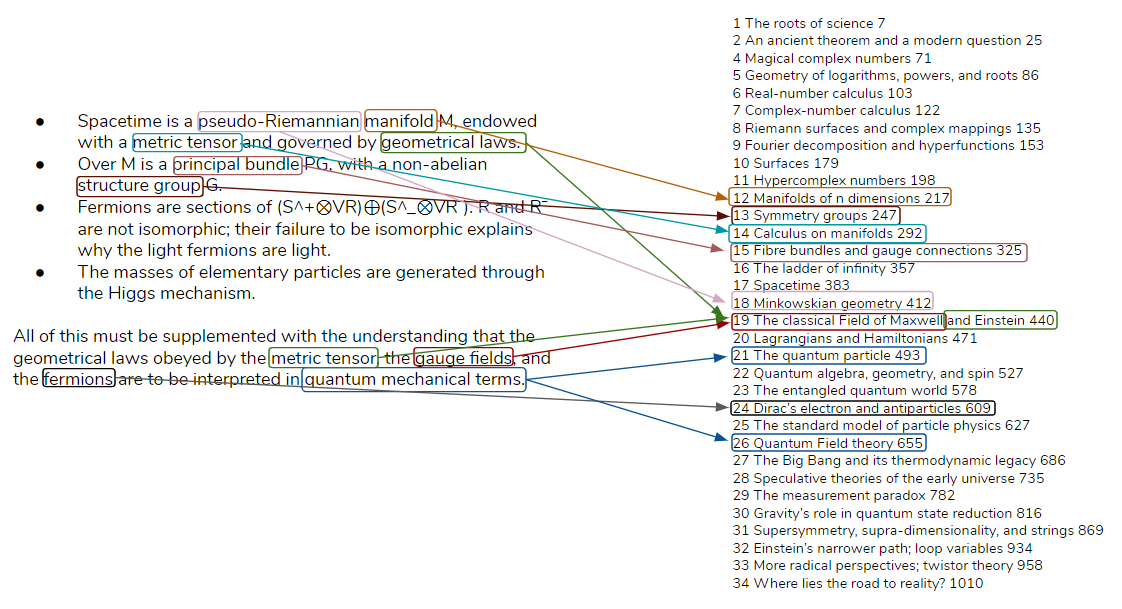
Direct Connections between the Graph, the Wall, and the Tome

Connections between the Graph and the Wall

Graph->Wall connections suggested by Eric Weinstein

Alternative representation of the Graph->Wall connections suggested by Eric Weinstein

Alternative Graph->Wall Connections

The following figure connects the Graph to elements on the Wall. There are certain holes since there aren't visualizations or formulas for all concepts mentioned in the Graph.

Alternative representation of the connections between the Graph and the Wall

The following figure connects the Graph to elements on the Wall. There are certain holes since there aren't visualizations or formulas for all concepts mentioned in the Graph.

Alternative representation of the connections between the Graph and the Wall

On the left-hand side, we have the Graph. On the right-hand side, there is a list of all elements that appear on the Wall.

Interactive representation of the connections between the Graph and the Wall

An interactive version of the Wall that shows direct connections to the graph is available here.

Connections between an updated Graph and updated Wall

In the following figure, the holes in the wall have been filled with appropriate illustrations and equations.

Connections between the Wall and the Tome

Connections between Wall and Tome

On the left-hand side, we have a list of all elements that appear on the Wall and on the right-hand side we have the table of contents of the Tome. Only connections between concepts that are also mentioned in the Graph are shown.

Connections between the Graph and the Tome

Connections between Graph and Tome

On the left-hand side, we have the Graph and on the right-hand side we have the table of contents of the Tome.

Resources

• Eric Weinstein's Geometric Unity project.