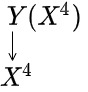Difference between revisions of "Observerse"
(Created page with "category:Ericisms") |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[ | The '''observerse''' is the central mathematical object in the [[Theory of Geometric Unity]]. It is a mapping from a four-dimensional manifold \(X^4\) to a manifold \(Y\), which replaces Einstein's spacetime. There are four different constructions of the observerse: exogenous, bundle-theoretic, endogenous, and tautological. Each generates a possible Geometric Unity theory. | ||
== Exogenous == | |||
In the observerse's exogenous construction, the manifold \(X^4\) includes into any manifold \(Y\) of four dimensions or higher which can admit it as an immersion. | |||
$$ X^4 \hookrightarrow Y $$ | |||
== Bundle-Theoretic == | |||
In the observerse's bundle-theoretic construction, the manifold \(Y\) sits over \(X^4\) as a fiber bundle. | |||
[[File:Observerse-Bundle-Theoretic.jpg]] | |||
== Endogenous == | |||
In the observerse's endogenous construction, \(Y\) is the space of metrics on the manifold \(X^4\). | |||
[[File:Observerse-Endogenous.jpg]] | |||
== Tautological == | |||
In the observerse's tautological construction, the manifold \(X^4\) equals \(Y\). | |||
$$ X^4 = Y $$ | |||
[[Category:Geometric Unity]] | |||
[[Category:Ericisms]] | |||
Latest revision as of 01:20, 1 April 2021
The observerse is the central mathematical object in the Theory of Geometric Unity. It is a mapping from a four-dimensional manifold \(X^4\) to a manifold \(Y\), which replaces Einstein's spacetime. There are four different constructions of the observerse: exogenous, bundle-theoretic, endogenous, and tautological. Each generates a possible Geometric Unity theory.
Exogenous
In the observerse's exogenous construction, the manifold \(X^4\) includes into any manifold \(Y\) of four dimensions or higher which can admit it as an immersion.
$$ X^4 \hookrightarrow Y $$
Bundle-Theoretic
In the observerse's bundle-theoretic construction, the manifold \(Y\) sits over \(X^4\) as a fiber bundle.
Endogenous
In the observerse's endogenous construction, \(Y\) is the space of metrics on the manifold \(X^4\).
Tautological
In the observerse's tautological construction, the manifold \(X^4\) equals \(Y\).
$$ X^4 = Y $$