Graph, Wall, Tome

The Assignment

There are 3 different pieces of the puzzle that Eric Weinstein pointed to during a call on Discord: graph, wall and tome. Please hold on to this information, that is they’re not public yet, until they come up in a dedicated future episode on The Portal. In the meantime, feel free to try to figure out how they fit together and what you can do with them in order to understand reality. Also, trying to answer the questions at the end helps you get started.

This was first collected in a Google Doc titled Graph, Wall, Tome - Problem Solving.

The Graph

The paragraph by Edward Witten as posted by Eric via Twitter.

However, there are 3 flaws with it:

• In (ii), “vector bundle X” should be changed to principal G-bundle.
• Also in (ii), “nonabelian gauge group G” should be changed to nonabelian structure group G.
• In (iii), R and R should be (complex) linear representations of G and so they are not equivalent.

Converted to text and re-written according to 'flaws'

If one wants to summarise our knowledge of physics in the briefest possible terms, there three really fundamental observations:

1. Spacetime is a pseudo-Riemannian manifold M, endowed with a metric tensor and governed by geometrical laws.
2. Over M is a principle bundle $$P_{G}$$ with a non-abelian structure group G.
3. Fermions are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}\_ \otimes V_{\bar{R}})$$. $$R$$ and $$\bar{R}$$ are not isomorphic; their failure to be isomorphic explains why the light fermions are light.
4. Add something about Higgs

All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.

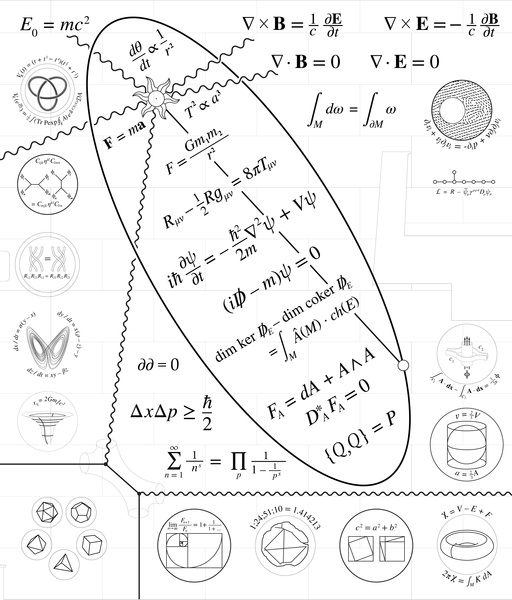
The Wall

Source

Eric talked about some of the important equations on the wall. There are 2 different recorded versions of the conversation if you want to listen to it.

Expansion

1: Einstein's General Relativity equation:

$$R_{\mu v}-\frac{1}{2}Rg_{\mu v} = 8 \pi T_{\mu v}$$

2: Maxwell's equations:

$$\nabla \times \mathbf{B} = \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t}$$

$$\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}}{\partial t}$$

$$\nabla \cdot \mathbf{B} = 0$$

$$\nabla \cdot \mathbf{E} = 0$$

2: Yang-Mills equations:

$$d^*_A F_A \propto J$$

3: Dirac equation:

$$(i \not{D}_A - m)\psi = 0$$

4: Klein-Gordon equation:

$$\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \psi - \nabla^2 \psi + \frac{m^2 c^2}{\hbar^2} \psi = 0$$

Einstein's mass-energy equation:

$$E = mc^2$$

Kepler's 2nd law:

$$\frac{d\theta}{dt} \propto \frac{1}{r^2}$$

Newton's force-acceleration equation:

$$\mathbf{F} = m\mathbf{a}$$

Keplers 3rd law:

$$T^2 \propto a^3$$

Newtons gravitational law:

$$F = \frac{G m_1 m_2}{r^2}$$

Schrodinger's equation:

$$i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2)}{2 m} \nabla^2 \psi + V \psi$$

Atiyah-Singer theorem:

$$dim\, ker \not{D}_E - dim \, coker \not{D}_E = \int_M \hat{A}(M) \cdot ch(E)$$

Defining relation of supersymmetry:

$$\{Q,Q\} = P$$

Stokes' theorem:

$$\int_M d\omega = \int_{\partial M}\omega$$

The boundary of a boundary is zero:

$$\partial\partial = 0$$

Heisenberg's indeterminacy relation:

$$\Delta x \Delta p \geq \frac{\hbar}{2}$$

Euler's formula for Zeta-function:

$$\sum\limits_{n=1}^{\infty} \frac{1}{n^{s}} = \prod\limits_{p} \frac{1}{1 - \frac{1}{p^s}}$$

The Tome

ISBN: 978-0679776314

• Road to Reality by Roger Penrose (2004)
• There appears to be a Kindle Edition that isn't available. If anyone in the community has a way to get an electronic version of the book, please add it here.
• Purchase the book somehow, then get the pdf here

Questions

Some questions Eric posed related to the assignment:

What is $$F_A$$ geometrically?

Atiyah-Singer index theorem

What are $$R$$ and $$\bar{R}$$ geometrically?(todo, wrong subscripts)

Einstein field equaitions Einstein’s original publication, Die Feldgleichungen der Gravitation, in English

How do they relate?

Cohomologhy

What does this have to do with Penrose Stairs?

• Penrose stairs
• Spinor

We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.

What are “Horizontal Subspaces” and what do they have to do with Vector Potentials or Gauge fields?

• Vertical and horizontal bundles
• Introduction to gauge theory
• Symmetry

From theplebistocrat:

Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.

Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.

But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.

Resources & References

• Recording of original call w/ Eric
• Book Recommendations