Difference between revisions of "Decoding the Graph-Wall-Tome Connection"
| (42 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{InfoboxProject | |||
|project=Graph-Wall-Tome Connection | |||
|image=[[File:Ascending and Descending.jpg]] | |||
|topic=[[Graph, Wall, Tome]] | |||
|leader=Aardvark | |||
|startdate=21 April 2020 | |||
|customlabel1=New Graph-Wall Mind Map | |||
|customdata1=[https://drive.google.com/file/d/1ZMT8nDyF6qT5nh6hiCjrHyX4giKKmGSA/view?usp=sharing Link] | |||
|customlabel2=Graph Mind Map | |||
|customdata2=[https://drive.google.com/file/d/16r60-56mhYCx4KKBvZv_6HDLOLw43X7y/view?usp=sharing Link] | |||
|customlabel3=Google Drive | |||
|customdata3=[https://drive.google.com/drive/folders/1706CBEJQEMppV60OU8OtcXxicluk2T3Y?usp=sharing Drive] | |||
|customlabel4=Master Planning | |||
|customdata4=[https://docs.google.com/document/d/1t9AvvFZzODw1WiGRZwRsFFZdPdBzYVJGLHiqWNrMtIA/edit?usp=sharing Doc] | |||
|link1title=Website | |||
|link1=[https://graphwalltome.com/ Homepage] | |||
|link2title= | |||
|link2= | |||
|link3title= | |||
|link3= | |||
|link4title=Discord | |||
|link4=[https://discord.gg/Z3u3pPm Invite] | |||
}} | |||
An important aspect of the [[Graph, | An important aspect of the [[Graph, Wall, Tome#Prime Directive|prompt]] is that neither the [[Graph, Wall, Tome#Graph|Graph]], nor the [[Graph, Wall, Tome#Wall|Wall]] or the [[Graph, Wall, Tome#Tome|Tome]] are that important on their own. Only together does their explanatory power exceed the limits of any part alone. The common threads that run through all of them are what matter: what is common among them is what should be expanded, and what is particular to one should be promoted and developed if it is a part of fundamental physics toolkit, or removed if it isn't. | ||
The goals of this project are to: | The goals of this project are to: | ||
* Identify the common threads in the Graph, Wall, and Tome. | * Identify the common threads (the "unifying idea") in the Graph, Wall, and Tome. These will indicate how to [[Editing the Graph|Edit the Graph]] and [[Defacing the Wall|Deface the Wall]]. | ||
* Create and collect resources that make it easy to understand them. | * Create and collect resources that make it easy to understand them, thus contributing to [[Rewriting the Tome]]. | ||
== Guiding Questions and Comments by Eric Weinstein == | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:400px; overflow:auto;"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:400px; overflow:auto;"> | ||
<div style="font-weight:bold;line-height:1.6;">What is $$F_A$$ geometrically?</div> | <div style="font-weight:bold;line-height:1.6;">What is $$F_A$$ geometrically?</div> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
$$F_A$$ is the curvature tensor associated | $$F_A$$ is the curvature tensor associated with the connection or vector potential $$A$$. | ||
</div></div> | </div></div> | ||
| Line 20: | Line 40: | ||
<div style="font-weight:bold;line-height:1.6;">What are $$R_{\mu v}$$ and $$R$$ geometrically?</div> | <div style="font-weight:bold;line-height:1.6;">What are $$R_{\mu v}$$ and $$R$$ geometrically?</div> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
[https://www.youtube.com/watch?v=UfThVvBWZxM&t=12m6s Explanation of $$R$$] | [https://www.youtube.com/watch?v=UfThVvBWZxM&t=12m6s Explanation of $$R$$] | ||
| Line 30: | Line 49: | ||
The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts. | The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts. | ||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:400px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Further thoughts on the meaning of R</div> | |||
<div class="mw-collapsible-content"> | |||
Computing length in non-orthogonal bases | |||
First, just describing the length of a vector on a curved space is hard. It is given by: | |||
$$Length^{squared} = g_{11}dX^{1}dX^{1} + g_{12}dX^{1}dX^{2} + g_{21}dX^{2}dX^{1} + g_{22}dX^{2}dX^{2}$$ | |||
Some notes: | |||
* This is not Pythagorean theorem, because $$dX^{1}$$ and $$dX^{2}$$ are not perpendicular. | |||
* Instead, looks like a formula to get the diagonal from two opposite vertices in a parallelogram. | |||
* If $$dX^{1}$$ and $$dX^{2}$$ are perpendicular, then $$g_{12}$$ and $$g_{21}$$ would be 0, and we would get $$Length^{squared} = g_{11}(dX^{1})^{2} + g_{22}(dX^{2})^{2}$$ | |||
* See: [https://www.youtube.com/watch?v=UfThVvBWZxM&t=14m27s the video @ 14m27s] | |||
Computing vector rotation due to parallel transport | |||
Then, they show parallel transport when following a parallelogram, but over a curved 3D manifold. To compute the vector rotation by components, they show: | |||
$$dV^{1} = dX^{1}dX^{2} (V^{1}R^{1}_{112} + V^{2}R^{1}_{212} + V^{3}R^{1}_{312})$$ | |||
$$dV^{2} = dX^{1}dX^{2} (V^{1}R^{2}_{112} + V^{2}R^{2}_{212} + V^{3}R^{2}_{312})$$ | |||
$$dV^{3} = dX^{1}dX^{2} (V^{1}R^{3}_{112} + V^{2}R^{3}_{212} + V^{3}R^{3}_{312})$$ | |||
or, using $$i$$ to summarize across all 3 components (difference vectors): | |||
$$dV^{i} = dX^{1}dX^{2} (V^{1}R^{i}_{112} + V^{2}R^{i}_{212} + V^{3}R^{i}_{312})$$ | |||
or , using $$j$$ to index over all 3 components (original vector): | |||
$$dV^{i} = dX^{1}dX^{2} \Sigma_{j} [(V^{j}R^{i}_{j12}]$$ | |||
See: [https://www.youtube.com/watch?v=UfThVvBWZxM&t=19m33s the video @ 19m33s] | |||
Open questions: | |||
* Why a parallelogram? | |||
* How to properly overlay the parallelogram onto the 3d manifold, in order to do the parallel transport? | |||
* How does this relate to the length computation above? | |||
Putting it all together | |||
Now, moving to 4D, we can compute $$R_{\mu v}$$ as: | |||
$$R_{00} = R^{0}_{000} + R^{1}_{010} + R^{2}_{020} + R^{3}_{030}$$ | |||
$$R_{10} = R^{0}_{100} + R^{1}_{110} + R^{2}_{120} + R^{3}_{130}$$ | |||
$$R_{01} = R^{0}_{001} + R^{1}_{011} + R^{2}_{021} + R^{3}_{030}$$ | |||
etc. | |||
Indexing i over all 4 component vectors / dimensions, we get: | |||
$$R_{00} = \Sigma_{i} R^{i}_{0i0}$$ | |||
$$R_{10} = \Sigma_{i} R^{i}_{1i0}$$ | |||
$$R_{01} = \Sigma_{i} R^{i}_{0i1}$$ | |||
etc. | |||
Summarizing on $$\mu$$, we get: | |||
$$R_{\mu 0} = \Sigma_{i} R^{i}_{\mu i0}$$ | |||
$$R_{\mu 1} = \Sigma_{i} R^{i}_{\mu i1}$$ | |||
etc | |||
Summarizing on $$v$$, we get: | |||
$$R_{\mu v} = \Sigma_{i} R^{i}_{\mu iv}$$ | |||
Open questions: | |||
* If we hadn't moved from 3D to 4D, what would this all have looked like? | |||
* What does this have to do with the parallelogram? | |||
* Why are there two indices? | |||
</div></div> | </div></div> | ||
| Line 68: | Line 171: | ||
</blockquote> | </blockquote> | ||
</div></div> | </div></div> | ||
<blockquote>"The source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language." - Eric Weinstein </blockquote> | |||
* Another valuable resource is the [[Talk:Graph,_Wall,_Tome#EricRWeinstein_2020-02-02_at_1:31_PM|comments Eric made regarding how the Wall should be modified]]. | |||
== Direct Connections between the Graph, the Wall, and the Tome == | |||
=== Connections between the Graph and the Wall=== | |||
<div class="toccolours mw-collapsible" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Graph->Wall connections suggested by Eric Weinstein</div> | |||
<div class="mw-collapsible-content"> | |||
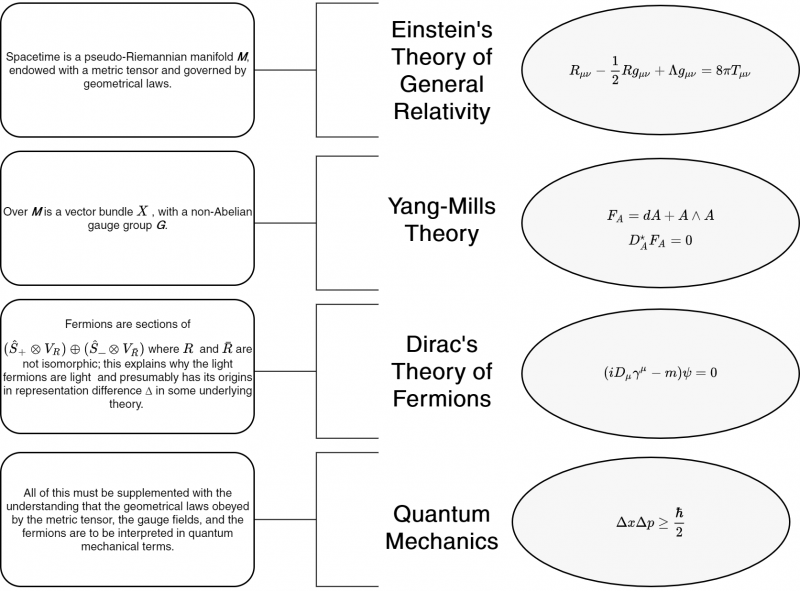
[[File:Graph To Wall eric.png|800px|center]] | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Alternative representation of the Graph->Wall connections suggested by Eric Weinstein</div> | |||
<div class="mw-collapsible-content"> | |||
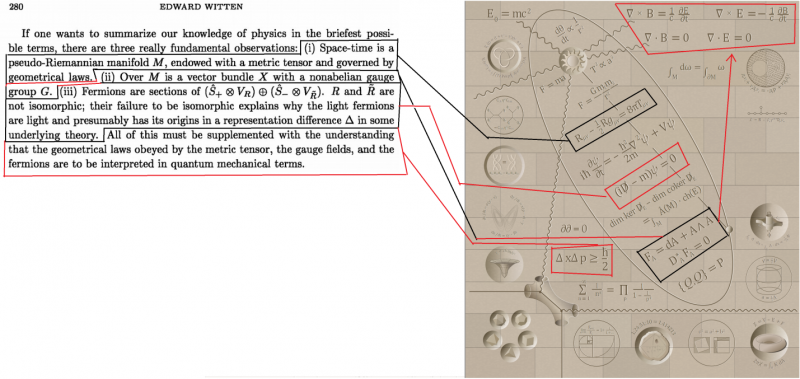
[[File:Bad Version of Graph to Wall.png|800px|center]] | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Alternative Graph->Wall Connections</div> | |||
<div class="mw-collapsible-content"> | |||
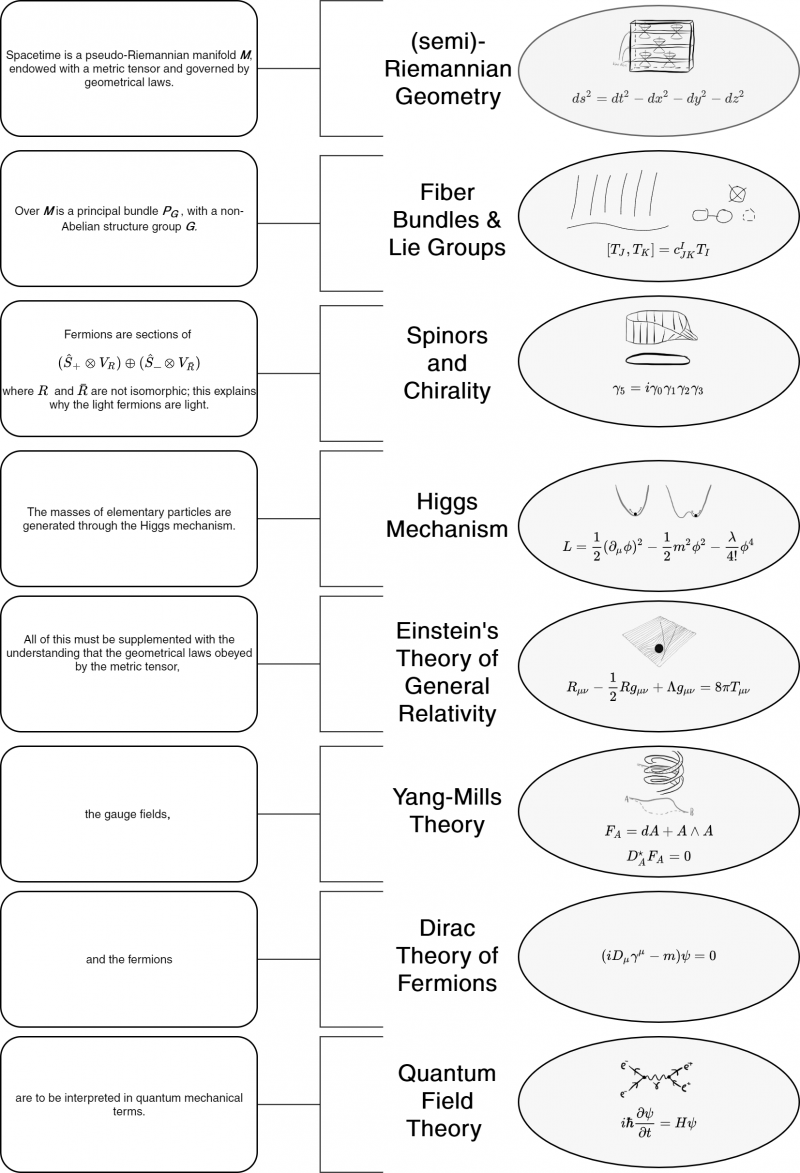
The following figure connects the Graph to elements on the Wall. There are certain holes since there aren't visualizations or formulas for all concepts mentioned in the Graph. | |||
[[File:Graph To Wall original.png|800px|center]] | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Alternative representation of the connections between the Graph and the Wall</div> | |||
<div class="mw-collapsible-content"> | |||
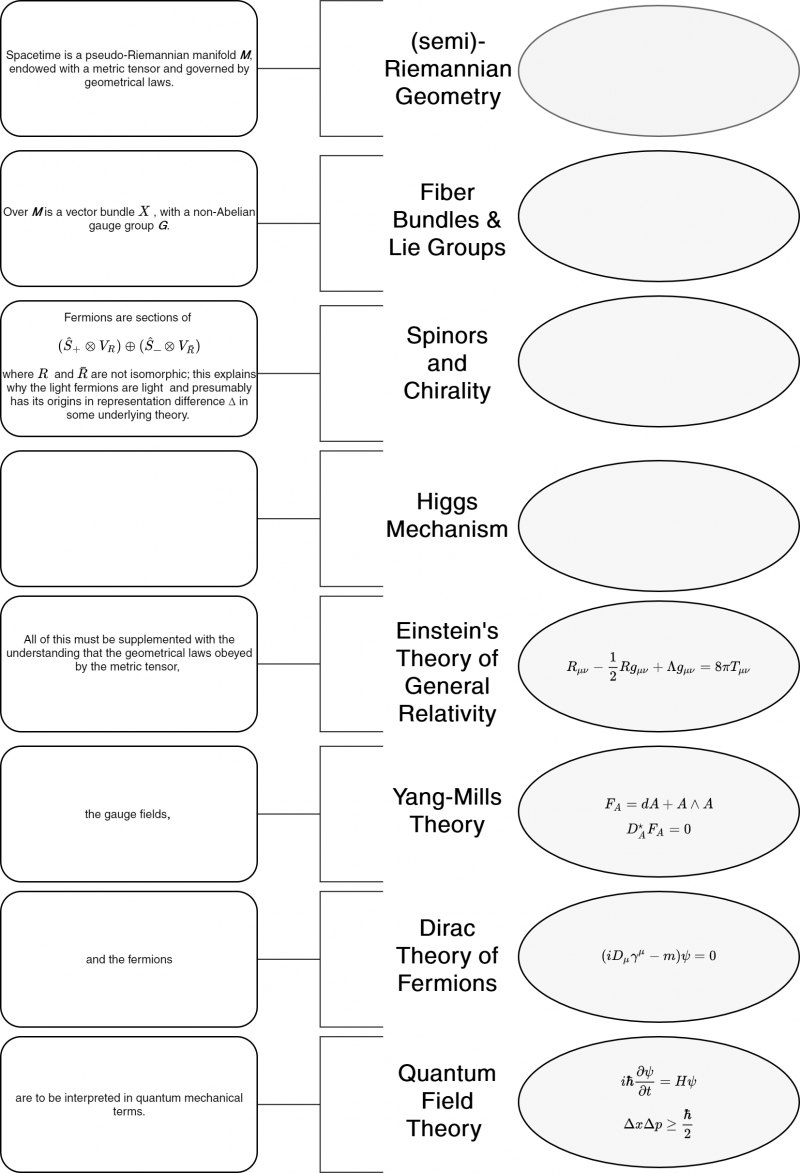
The following figure connects the Graph to elements on the Wall. There are certain holes since there aren't visualizations or formulas for all concepts mentioned in the Graph. | |||
[[File:Graph To Wall original.png|800px|center]] | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Alternative representation of the connections between the Graph and the Wall</div> | |||
<div class="mw-collapsible-content"> | |||
On the left-hand side, we have the [[Graph,_Wall,_Tome#The_Graph|Graph]]. On the right-hand side, there is a list of all elements that appear on the [[Graph,_Wall,_Tome#The_Wall|Wall]]. | |||
[[File:Graph-Wall connections.png|center]] | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Interactive representation of the connections between the Graph and the Wall</div> | |||
<div class="mw-collapsible-content"> | |||
An interactive version of the Wall that shows direct connections to the graph is available [https://dev.theportal.dev/wall/ here]. | |||
</div></div> | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Connections between an updated Graph and updated Wall</div> | |||
<div class="mw-collapsible-content"> | |||
In the following figure, the holes in the wall have been filled with appropriate illustrations and equations. | |||
[[File:Graph To Wall.png|800px|center]] | |||
</div></div> | |||
=== Connections between the Wall and the Tome === | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Connections between Wall and Tome</div> | |||
<div class="mw-collapsible-content"> | |||
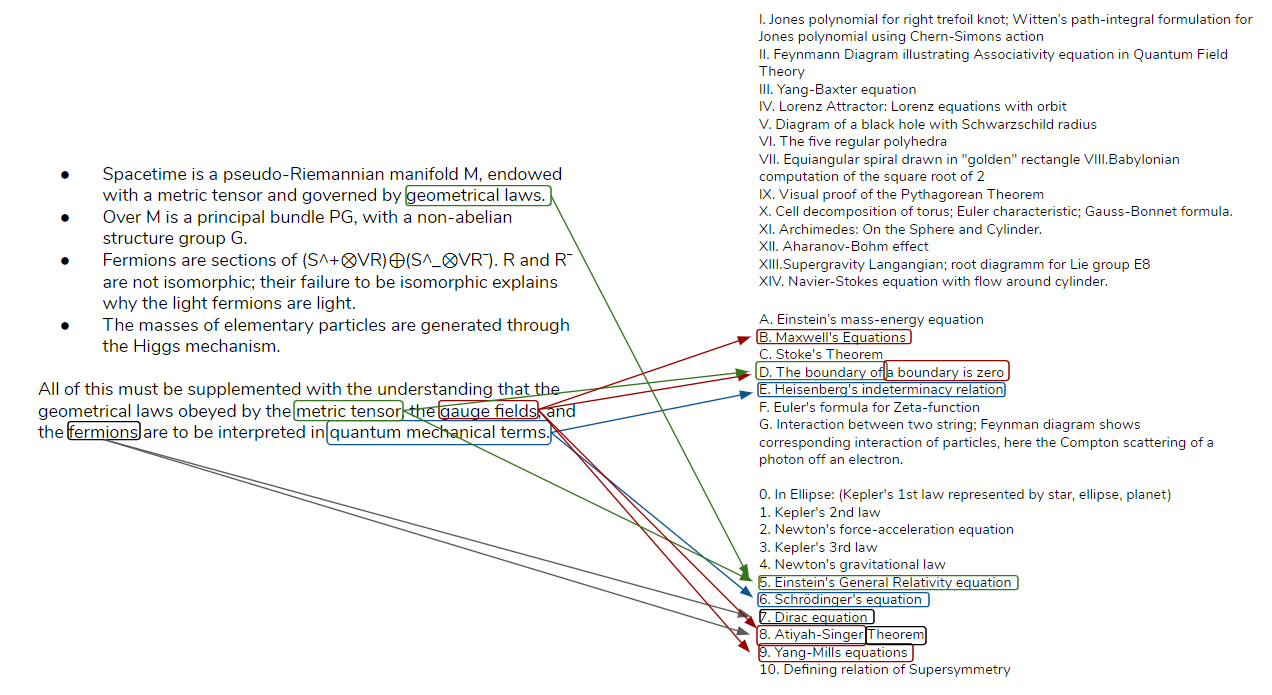
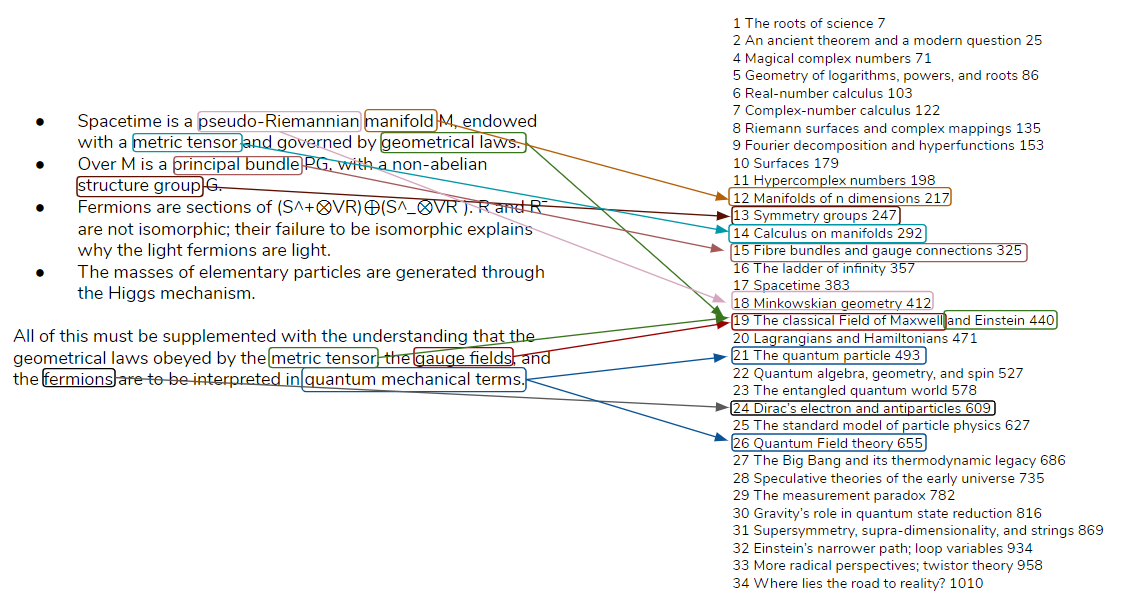
On the left-hand side, we have a list of all elements that appear on the [[Graph,_Wall,_Tome#The_Wall|Wall]] and on the right-hand side we have the table of contents of the [[Graph,_Wall,_Tome#The_Tome|Tome]]. Only connections between concepts that are also mentioned in the Graph are shown. | |||
[[File:Wall-Tome Connections.png|center]] | |||
</div></div> | |||
=== Connections between the Graph and the Tome === | |||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px; overflow:auto;"> | |||
<div style="font-weight:bold;line-height:1.6;">Connections between Graph and Tome</div> | |||
<div class="mw-collapsible-content"> | |||
On the left-hand side, we have the [[Graph,_Wall,_Tome#The_Graph|Graph]] and on the right-hand side we have the table of contents of the [[Graph,_Wall,_Tome#The_Tome|Tome]]. | |||
[[File:Graph-Tome Connection.png|center]] | |||
</div></div> | |||
== Resources == | |||
* [https://drive.google.com/file/d/1ZMT8nDyF6qT5nh6hiCjrHyX4giKKmGSA/view?usp=sharing New Graph-Wall Mind Map] | |||
* [https://drive.google.com/file/d/16r60-56mhYCx4KKBvZv_6HDLOLw43X7y/view?usp=sharing Map of Witten's Physics and Geometry Essay] | |||
* [https://docs.google.com/document/d/1t9AvvFZzODw1WiGRZwRsFFZdPdBzYVJGLHiqWNrMtIA/edit?usp=sharing Master Planning Doc] | |||
* [https://drive.google.com/drive/folders/1706CBEJQEMppV60OU8OtcXxicluk2T3Y?usp=sharing Drive Folder] | |||
* [https://docs.google.com/document/d/18rN-zfv41xeH3WFNOrZNb7Clz-yu1dgulP4bcEPKbcY/edit?usp=sharing List of Reference Material] | |||
[[Category:Graph, Wall, Tome]] | |||
[[Category:Projects]] | |||
Latest revision as of 01:12, 22 January 2021
| Graph-Wall-Tome Connection | |

| |
| Information | |
|---|---|
| Topic | Graph, Wall, Tome |
| Leader | Aardvark |
| Start Date | 21 April 2020 |
| New Graph-Wall Mind Map | Link |
| Graph Mind Map | Link |
| Google Drive | Drive |
| Master Planning | Doc |
| Links | |
| Website | Homepage |
| Discord | Invite |
| All Projects | |
An important aspect of the prompt is that neither the Graph, nor the Wall or the Tome are that important on their own. Only together does their explanatory power exceed the limits of any part alone. The common threads that run through all of them are what matter: what is common among them is what should be expanded, and what is particular to one should be promoted and developed if it is a part of fundamental physics toolkit, or removed if it isn't.
The goals of this project are to:
- Identify the common threads (the "unifying idea") in the Graph, Wall, and Tome. These will indicate how to Edit the Graph and Deface the Wall.
- Create and collect resources that make it easy to understand them, thus contributing to Rewriting the Tome.
Guiding Questions and Comments by Eric Weinstein
$$F_A$$ is the curvature tensor associated with the connection or vector potential $$A$$.
$$R$$ is a scalar value, describing the "curvature of the spacetime manifold" at each point along the manifold. It's based on a concept of 'parallel transport', where you move a vector around some path on the manifold.
$$R$$ can be computed at each point on the manifold, and describes the difference in the vector's angle after following an infinitesimally small path around the neighborhood of that point, vs. what it was originally. The video does a great job of visualizing when and why that vector angle change would happen, with flat vs. curved manifolds.
In the video, they focus first on the curvature of space. Hopefully they incorporate back in curvature in time, because that's less obvious.
The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts.
Computing length in non-orthogonal bases
First, just describing the length of a vector on a curved space is hard. It is given by:
$$Length^{squared} = g_{11}dX^{1}dX^{1} + g_{12}dX^{1}dX^{2} + g_{21}dX^{2}dX^{1} + g_{22}dX^{2}dX^{2}$$
Some notes:
- This is not Pythagorean theorem, because $$dX^{1}$$ and $$dX^{2}$$ are not perpendicular.
- Instead, looks like a formula to get the diagonal from two opposite vertices in a parallelogram.
- If $$dX^{1}$$ and $$dX^{2}$$ are perpendicular, then $$g_{12}$$ and $$g_{21}$$ would be 0, and we would get $$Length^{squared} = g_{11}(dX^{1})^{2} + g_{22}(dX^{2})^{2}$$
- See: the video @ 14m27s
Computing vector rotation due to parallel transport
Then, they show parallel transport when following a parallelogram, but over a curved 3D manifold. To compute the vector rotation by components, they show:
$$dV^{1} = dX^{1}dX^{2} (V^{1}R^{1}_{112} + V^{2}R^{1}_{212} + V^{3}R^{1}_{312})$$
$$dV^{2} = dX^{1}dX^{2} (V^{1}R^{2}_{112} + V^{2}R^{2}_{212} + V^{3}R^{2}_{312})$$
$$dV^{3} = dX^{1}dX^{2} (V^{1}R^{3}_{112} + V^{2}R^{3}_{212} + V^{3}R^{3}_{312})$$
or, using $$i$$ to summarize across all 3 components (difference vectors):
$$dV^{i} = dX^{1}dX^{2} (V^{1}R^{i}_{112} + V^{2}R^{i}_{212} + V^{3}R^{i}_{312})$$
or , using $$j$$ to index over all 3 components (original vector):
$$dV^{i} = dX^{1}dX^{2} \Sigma_{j} [(V^{j}R^{i}_{j12}]$$
See: the video @ 19m33s
Open questions:
- Why a parallelogram?
- How to properly overlay the parallelogram onto the 3d manifold, in order to do the parallel transport?
- How does this relate to the length computation above?
Putting it all together
Now, moving to 4D, we can compute $$R_{\mu v}$$ as:
$$R_{00} = R^{0}_{000} + R^{1}_{010} + R^{2}_{020} + R^{3}_{030}$$
$$R_{10} = R^{0}_{100} + R^{1}_{110} + R^{2}_{120} + R^{3}_{130}$$
$$R_{01} = R^{0}_{001} + R^{1}_{011} + R^{2}_{021} + R^{3}_{030}$$
etc.
Indexing i over all 4 component vectors / dimensions, we get:
$$R_{00} = \Sigma_{i} R^{i}_{0i0}$$
$$R_{10} = \Sigma_{i} R^{i}_{1i0}$$
$$R_{01} = \Sigma_{i} R^{i}_{0i1}$$
etc.
Summarizing on $$\mu$$, we get:
$$R_{\mu 0} = \Sigma_{i} R^{i}_{\mu i0}$$
$$R_{\mu 1} = \Sigma_{i} R^{i}_{\mu i1}$$
etc
Summarizing on $$v$$, we get:
$$R_{\mu v} = \Sigma_{i} R^{i}_{\mu iv}$$
Open questions:
- If we hadn't moved from 3D to 4D, what would this all have looked like?
- What does this have to do with the parallelogram?
- Why are there two indices?
We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.
From theplebistocrat:
Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.
Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.
But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.
"The source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language." - Eric Weinstein
- Another valuable resource is the comments Eric made regarding how the Wall should be modified.
Direct Connections between the Graph, the Wall, and the Tome
Connections between the Graph and the Wall
An interactive version of the Wall that shows direct connections to the graph is available here.
Connections between the Wall and the Tome
Connections between the Graph and the Tome