Difference between revisions of "The Road to Reality Study Notes"
| Line 75: | Line 75: | ||
The geometer Eugenio Beltrami is introduced as having discovered a geometric method relating these different hyperbolic representations which involve projections from the plane to spherical surfaces and back. Imagine the hyperbolic plane cuts a sphere at the equator. ''Hemispheric'' representation is the hyperbolic geometry representation on the northern hemisphere of the Beltrami sphere, found from projecting the ''projective'' representation upward onto its surface. Straight Euclidean lines in the plane are now semicircles which meet the equator orthogonally. Stereographic projection is introduced with the example of projecting these semicircles back onto the plane but projecting from the point of the south pole. This gives beautifully gives us the ''conformal'' representation on the plane. Two important properties of stereographic projection are: | The geometer Eugenio Beltrami is introduced as having discovered a geometric method relating these different hyperbolic representations which involve projections from the plane to spherical surfaces and back. Imagine the hyperbolic plane cuts a sphere at the equator. ''Hemispheric'' representation is the hyperbolic geometry representation on the northern hemisphere of the Beltrami sphere, found from projecting the ''projective'' representation upward onto its surface. Straight Euclidean lines in the plane are now semicircles which meet the equator orthogonally. Stereographic projection is introduced with the example of projecting these semicircles back onto the plane but projecting from the point of the south pole. This gives beautifully gives us the ''conformal'' representation on the plane. Two important properties of stereographic projection are: | ||
* Conformal, so angles are preserved | |||
* Sends circles on the sphere to circles on the plane | |||
It is then emphasized that each of these representations are merely ‘Euclidean models’ of hyperbolic geometry and are not to be taken as what the geometry actually ‘is’. In fact, there are more representations such as the [https://en.wikipedia.org/wiki/Minkowski_space Minkowskian geometry] of special relativity. The idea of a generalized ‘square’ is then presented in ''conformal'' and ''projective'' hyperbolic representations to show an interesting generalization of the Euclidean square. | It is then emphasized that each of these representations are merely ‘Euclidean models’ of hyperbolic geometry and are not to be taken as what the geometry actually ‘is’. In fact, there are more representations such as the [https://en.wikipedia.org/wiki/Minkowski_space Minkowskian geometry] of special relativity. The idea of a generalized ‘square’ is then presented in ''conformal'' and ''projective'' hyperbolic representations to show an interesting generalization of the Euclidean square. | ||
Revision as of 14:51, 6 June 2020
Each week The Road to Reality Book Club tackles a chapter of Sir Roger Penrose's Epic Tome. We use these meetings as an opportunity to write down the major points to be taken from our reading. Here we attempt to sum up what we believe Penrose was trying to convey and why. The hope is that these community-generated reading notes will benefit people in the future as they go on the same journey.
Other Resources
- The Portal Book Club - We have a weekly group that meets to talk about this book. Come join us in Discord!
- Reference Material by Chapter on the Wiki
- Chronological guide to concepts introduced in TRTR Google Doc
- Book Club Resources in Google Drive
Chapter 1 The Roots of Science
1.1 The quest for the forces that shape the world
Understanding natural processes has been a common pursuit since the dawn of humanity. After many millennia of chaos and frustration, it was discovered that the regular movement of celestial bodies, such as the sun and moon, could be described mathematically. It became apparent that mathematics unlocked deep truths about the universe. Many people in ancient times allowed their imaginations to be carried away by their fascination with the subject, leading to mystical associations with mathematical objects. One famous example from the ancient Greeks is the association between Platonic solids and the basic elementary states of matter.
1.2 Mathematical truth
There was a need to define a more rigorous method for differentiating truth claims. The Greek philosopher Thales of Miletus (c. 625-547 BC) and Pythagoras of Samos (c. 572-497 BC) are considered to be the first to introduce the concept of mathematical proof. Developing a rigorous mathematical framework was central to the development of science. Mathematical proof allowed for much stronger statements to be made about relationships between the arithmetic of numbers and the geometry of physical space.
A mathematical proof is essentially an argument in which one starts from a mathematical statement, which is taken to be true, and using only logical rules arrives at a new mathematical statement. If the mathematician hasn't broken any rules then the new statement is called a theorem. The most fundamental mathematical statements, from which all other proofs are built, are called axioms and their validity is taken to be self-evident. Mathematicians trust that the axioms, on which their theorems depend, are actually true. The Greek philosopher Plato (c.429-347 BC) believed that mathematical proofs referred not to actual physical objects but to certain idealized entities. Physical manifestations of geometric objects could come close to the Platonic world of mathematical forms, but they were always approximations. To Plato the idealized mathematical world of forms was a place of absolute truth, but inaccessible from the physical world.
1.3 Is Plato's mathematical world "real"?
Penrose asks us to consider if the world of mathematics in any sense real. He claims that objective truths are revealed through mathematics and that it is not a subjective matter of opinion. He uses Fermat's last theorem as an point to consider what it would mean for mathematical statements to be subjective. He shows that "the issue is the objectivity of the Fermat assertion itself, not whether anyone’s particular demonstration of it (or of its negation) might happen to be convincing to the mathematical community of any particular time". Penrose introduces a more complicated mathematical notion, the axiom of choice, which has been debated amongst mathematicians. He notes that "questions as to whether some particular proposal for a mathematical entity is or is not to be regarded as having objective existence can be delicate and sometimes technical". Finally he discusses the Mandelbrot set and claims that it exists in a place outside of time and space and was only uncovered by Mandelbrot. Any mathematical notion can be thought of as existing in that place. Penrose invites the reader to reconsider their notions of reality beyond the matter and stuff that makes up the physical world.
For further discussion from Penrose on this topic see Is Mathematics Invented or Discovered?
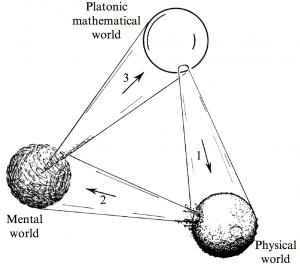
1.4 Three worlds and three deep mysteries
Penrose outlines his conception of three worlds:
- The Platonic Mathematical
- The Physical
- The Mental
as show in figure 1.3. Connections between these worlds present a great number of mysteries. The main focus of the book is to explore the connection between mathematics and its use in describing the physical world. Note that only a small subset of the mathematical world us utilized in describing the physical world. The reason why mathematics can describe the physical world so accurately is unknown. Moving in the counter clockwise direction there is a mysterious connection between the physical world and that of the mind. He believes that there must be some basis of consciousness in physical reality, but it is still unknown. Finally there is the connection between the mental world and mathematics. Penrose believes that there is no mathematical notion beyond our mental construction. He highlights that this figure represents many of his prejudices and might upset some people. Maybe the connections from one world do not fully describe the other, or are incomplete. Penrose believes that not much progress can be made with respect to the mental world until we know much more about the physical world.
1.5 The Good, the True, and the Beautiful
The full conception of Plato's theory of forms was not limited to only mathematical notions. Mathematics was linked to the concept of Truth but Plato was also interested in the absolute idealized forms of Beauty and Good. Beauty plays an important role in many mathematical discoveries and is often used as a guide to the truth. Questions of morality are of less relevance in this context but are critical with respect to the mental world. Moral debates are outside of the scope of this book but must be considered as science and technology progress. Penrose notes that figure 1.3 has purposely been constructed to be paradoxical in the sense that each world is entirely encompassed by the next. He writes "There may be a sense in which the three worlds are not separate at all, but merely reflect, individually, aspects of a deeper truth about the world as a whole of which we have little conception at the present time."
Chapter 2 An ancient theorem and a modern question
- summary
2.1 The Pythagorean theorem
To explore the process of pursuing mathematical truth, Penrose outlines a few proofs of the Pythagorean theorem. The theorem can be stated as such, "For any right-angled triangle, the squared length of the hypotenuse $$c$$ is the sum of the squared lengths of the other two sides $$a$$ and $$b$$ or in mathematical notation $$ a^2 + b^2 = c^2. $$
There are hundreds of proofs of the Pythagorean theorem but Penrose chooses to focus on two. The first involves filling up a plane with squares of two different sizes. Then adding a second pattern on top of tiled squares connecting the centers of the larger original squares. By translating the tilted pattern to the corner of the large square and observing the areas covered by the pattern you can show that the square on the hypotenuse is equal to the sum of the squares on the other two sides. While the outlined proof appears reasonable there are some implicit assumptions made. For instance what do you mean when we say square? What is a right angle?
2.2 Euclid's postulates
Euclid of Alexandria, sometimes referred to as the "father of geometry", was one of the first people to attempt to outline and document the assumptions that went into his geometrical arguments. Euclid broke these assumptions into two categories, axioms which were self-evident, essentially definitions, and a set of five postulates which were less certain, but appeared true. Penrose outlines the first 4 postulates as:
- There is a (unique) straight line segment connecting any two points.
- There is an unlimited (continuous) extendibility of any straight line segment.
- There existence a circle with any centre and with any value for its radius.
- There is equality of all right angles.
Euclid was trying to establish the rules which govern his geometry. Some interesting ideas start to emerge such as the indefinitely extendible geometric plane and the concept of congruence. Penrose writes "In effect, the fourth postulate is asserting the isotropy and homogeneity of space, so that a figure in one place could have the ‘same’ (i.e. congruent) geometrical shape as a figure in some other place". Surprisingly Euclid's first four postulates still align well with our understanding of a two-dimensional metric space.
Euclid's fifth postulate, also known as the parallel postulate, was more troublesome. In Penrose words "it asserts that if two straight line segments $$a$$ and $$b$$ in a plane both intersect another straight line $$c$$ (so that $$c$$ is what is called a transversal of $$a$$ and $$b$$) such that the sum of the interior angles on the same side of $$c$$ is less than two right angles, then $$a$$ and $$b$$, when extended far enough on that side of $$c$$, will intersect somewhere". One can see that the formulation of the fifth postulate is more complicated than the rest which lead to speculation of it's validity. With the fifth postulate one can go on to properly build a square and begin to explore the world of Euclidean geometry.
2.3 Similar-areas proof of the Pythagorean theorem
Penrose revisits the Pythagorean theorem by outlining another proof. Starting with a right triangle, subdivide the shape into two smaller triangles by drawing a line perpendicular to the hypotenuse through the right angle. The two smaller triangles are said to be similar to one another meaning they have the same shape but are different sizes. This is true because each of the smaller triangles has a right angle and shares an angle with the larger triangle. The third angle known because the sum of the angles in any triangle is always the same. Knowing that the sum of the area of the two small triangles equals the area of the big triangle (by construction), we can square the sides and show that the pythagorean theorem holds.
Again Penrose asks us to revisit our assumptions and examine which of Euclid's postulates were needed. Particularly our claim that the sum of the angles in a triangle add up to the same value of 180° (or $$\pi$$ radians). One must use the parallel postulate to show that this is true. Penrose asks us to consider what would it mean for the parallel postulate to be false? What would that imply? Would that make any sense? With these questions in mind we begin to explore a different kind of geometry.
2.4 Hyperbolic geometry: conformal picture
The topic of questioning fundamental assumptions is taken to a level deeper with the example of Euclid’s fifth postulate and hyperbolic geometry, illustrated with M.C. Escher’s Circle limit I. The notion that all the black and white fish near the boundary are equal in ‘size’ to the fish near the center starts the section with an interesting point of confusion between our visual perception of Euclidean geometry and the hyperbolic representation.
Within the hyperbolic plane, Euclid’s first four postulates hold true, however, the fifth parallel postulate is false. Penrose notes some interesting consequences of this are that the interior angles of a triangle do not add to π, the Pythagorean theorem fails to hold, and a given shape does not have a similar shape of a larger size. The idea of conformal representations is then introduced with the example that angular relations between lines in the Euclidean and this representation of the hyperbolic plane are precisely the same.
Penrose then gives us the relation between the interior angles of the hyperbolic triangle to its area and says that while there is a sense of ‘unpleasantness’ with the fact that the sum of the interior angles of a triangle within the hyperbolic frame do not add to π, there is something ‘elegant and remarkable’ in direct relation of these angles to the area of the triangle, which is impossible to show within the Euclidean framework. He then leaves us with the equation for hyperbolic distance and notes that with this, hyperbolic geometry has all the properties of Euclidean geometry apart from those that need the parallel postulate, and this allows us to form congruent shapes.
2.5 Other representations of hyperbolic geometry
Since hyperbolic geometry is a more abstract construct, the conformal representation presented in section 2.4 is not the only way to represent hyperbolic geometry in terms of Euclidean geometry. Projective representations are next presented, where the difference is that hyperbolic straight lines are now represented as Euclidean straight lines. The cost of this ‘simplification’ is that angles are no longer the same. Penrose gives the reader an equation which allows the projective geometry to be obtained from a radial expansion from the center of the conformal representation.
The geometer Eugenio Beltrami is introduced as having discovered a geometric method relating these different hyperbolic representations which involve projections from the plane to spherical surfaces and back. Imagine the hyperbolic plane cuts a sphere at the equator. Hemispheric representation is the hyperbolic geometry representation on the northern hemisphere of the Beltrami sphere, found from projecting the projective representation upward onto its surface. Straight Euclidean lines in the plane are now semicircles which meet the equator orthogonally. Stereographic projection is introduced with the example of projecting these semicircles back onto the plane but projecting from the point of the south pole. This gives beautifully gives us the conformal representation on the plane. Two important properties of stereographic projection are:
- Conformal, so angles are preserved
- Sends circles on the sphere to circles on the plane
It is then emphasized that each of these representations are merely ‘Euclidean models’ of hyperbolic geometry and are not to be taken as what the geometry actually ‘is’. In fact, there are more representations such as the Minkowskian geometry of special relativity. The idea of a generalized ‘square’ is then presented in conformal and projective hyperbolic representations to show an interesting generalization of the Euclidean square.
2.6 Historical aspects of hyperbolic geometry
2.7 Relation to physical space
Chapter 3 Kinds of number in the physical world
3.1 A pythagorean catastrophe?
3.2 The real number system
Natural Numbers:
‘Counting’ numbers from 1 to $$\infty$$.
Whole Numbers:
All counting numbers including 0, cannot be a fraction.
Integers:
All natural numbers and their negative counterparts and 0. If and are integers, then their sum , their difference , and their product are all integers (that is, the integers are closed under addition and multiplication), but their quotient may or may not be an integer, depending on whether can be divided by with no remainder.
Rational Numbers:
A number that can be expressed as the ratio a/b of two integers (or whole numbers) a and b, with b non-zero. The decimal expansion is alyas ultimately periodic, at a certain point the infinite sequence of digits consists of some finite sequence repeated indefinitely.
Irrational Numbers:
A number that cannot be expressed as the ratio of two integers. When an irrational number is expressed in decimal notation it never terminates nor repeats.
- Quadratic Irrational Numbers
- Arise in the solution of a general quadratic equation:
- <math>Ax^{2} + Bx + C = 0</math>
- With A non-zero, the solutions being (derived from the quadratic formula):
- <math>-\frac{B}{2A}\sqrt{\left(\frac{B}{2A}\right)^2}+\frac{C}{A}, \quad -\frac{B}{2A}\sqrt{\left(\frac{B}{2A}\right)^2}-\frac{C}{A}</math>
- where, to keep within the realm of real numbers, be must have B2 greater than 4AC. When A, B, and C are integers or rational numbers, and where there is no rational solution to the equation, the solutions are quadratic irrationals.
Real Numbers:
A number in the set of all numbers above that falls on the real number line. It can have any value.
- Algebraic Real Numbers:
- Any number that is the solution to a polynomial with rational coefficients.
- Transcendental Real Numbers
- Any number that is not the solution to a polynomial with rational coefficients.
3.3 Real numbers in the physical world
3.4 Do natural numbers need the physical world?
3.5 Discrete numbers in the physical world
Chapter 4 Magical Complex Numbers
Penrose introduced the complex numbers, extending addition, subtraction, multiplication, and division of the reals to the system obtained by adjoining i, the square root of -1. Polynomial equations can be solved by complex numbers, this property is called algebraic closure and follows from the Fundamental Theorem of Algebra.
Complex numbers can be visualized graphically as a plane, where the horizontal coordinate gives the real coordinate of the number and the vertical coordinate gives the imaginary part. This helps understand the behavior of power series; for example, the power series $$1-x^2+x^4+\cdots$$ converges to the function $$1/(1+x²)$$ only when $$|x|<1$$, despite the fact that the function doesn't seem to have "singular" behavior anywhere on the real line. This is explained by singularities at $$x=i,-i$$.
Finally, the Mandelbrot set is defined as the set of all points $$c$$ in the complex plane so that repeated applications of the transformation mapping $$z$$ to $$z^2+c$$, starting with $$z=0$$, do not escape to infinity.
Chapter 5 Geometry of logarithms, powers, and roots
This is a first pass of main topics in this chapter. This should be expanded.
5.1 Geometry of complex algebra
What addition and multiplication look like geometrically on a complex plane.
- law of addition
- law of multiplication
- addition map
- multiplication map
- what does multiply by i do? rotate
5.2 The idea of the complex logarithm
Relation between addition and multiplication when introducing exponents.
- $$b^{m+n} = b^m \times b^n$$
5.3 Multiple valuedness, natural logarithms
Different values can arrive at the same value. Rotation brings you back to the same place repeatedly.
- $$e^{i\theta}$$ is helpful notation for understanding rotating
- $$e^{i\theta} = cos \theta + i sin \theta$$
- (Worth looking into Taylor Series, which is related.)
Chapter 6 Real-number calculus
6.1 What makes an honest function?
- Differentiable, Analytic
6.2 Slopes of functions
- Derivative is the slope of the tangent line
- Finding the slope of the tangent line for every point
6.3 Higher derivatives; $$C^\infty$$-smooth functions
- Second derivatives
- Euler would require you to have functions that are $$C^\infty$$-smooth
- Not everything that is $$C^\infty$$-smooth is ok for Euler
6.4 The "Eulerian" notion of a function?
- Physics in trying to understand reality by approximating it.
6.5 The rules of differentiation
- Armed with these few rules (and loads and loads of practice), one can become an "expert at differentiation" without needing to have much in the way of actual understanding of why the rules work!
6.6 Integration
- Fundamental theory of calculus shows integration and differentiation are inverse operations.
- If we integrated then differentiate, we get the same answer back. Non-commutative the other way.