Difference between revisions of "Yang-Baxter equation"
(Created page with "<div class="floatright" style="text-align: center"> center|class=shadow|300px </div> In physics, the Yang–Baxter equation (or star–trian...") |
|||
| Line 6: | Line 6: | ||
:$${ ({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )=(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})}$$ | :$${ ({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )=(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})}$$ | ||
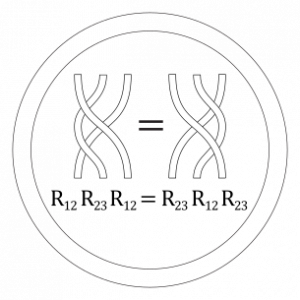
In one dimensional quantum systems, { | In one dimensional quantum systems, $${R}$$ is the scattering matrix and if it satisfies the Yang–Baxter equation then the system is integrable. The Yang–Baxter equation also shows up when discussing knot theory and the braid groups where $${R}$$ corresponds to swapping two strands. Since one can swap three strands two different ways, the Yang–Baxter equation enforces that both paths are the same. | ||
== Resources: == | == Resources: == | ||
*[https://en.wikipedia.org/wiki/Yang%E2%80%93Baxter_equation Yang-Baxter equation] | *[https://en.wikipedia.org/wiki/Yang%E2%80%93Baxter_equation Yang-Baxter equation] | ||
== Discussion: == | == Discussion: == | ||
Revision as of 22:25, 4 February 2020
In physics, the Yang–Baxter equation (or star–triangle relation) is a consistency equation which was first introduced in the field of statistical mechanics. It depends on the idea that in some scattering situations, particles may preserve their momentum while changing their quantum internal states. It states that a matrix {\displaystyle R}R, acting on two out of three objects, satisfies
- $${ ({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )=(\mathbf {1} \otimes {\check {R}})({\check {R}}\otimes \mathbf {1} )(\mathbf {1} \otimes {\check {R}})}$$
In one dimensional quantum systems, $${R}$$ is the scattering matrix and if it satisfies the Yang–Baxter equation then the system is integrable. The Yang–Baxter equation also shows up when discussing knot theory and the braid groups where $${R}$$ corresponds to swapping two strands. Since one can swap three strands two different ways, the Yang–Baxter equation enforces that both paths are the same.